El canal de YouTube dedicado a la psicología Bit Size Psych ha recuperado dos versiones de un problema clásico en un vídeo que se acerca a las 200.000 reproducciones y a los 500 comentarios después de apenas una semana.

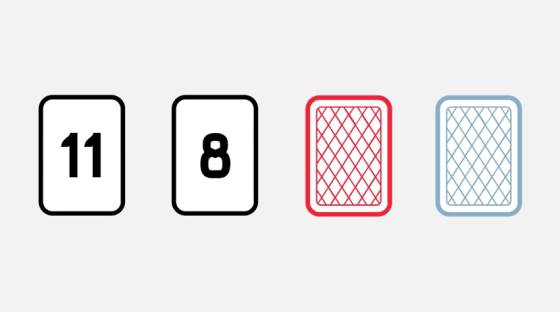
El primer acertijo que expone este vídeo consiste en encontrar la forma en la que, dando la vuelta al menor número de cartas posible, se pueda afirmar con seguridad si la siguiente frase es cierta o no: “Si una carta es par, su dorso es de color rojo”. No me extrañaría que hubieras visto antes este acertijo (o uno similar). Se trata de una variante de la llamada “tarea de selección de Wason”, una prueba clásica desarrollada el psicólogo inglés Peter C. Wason en 1966.
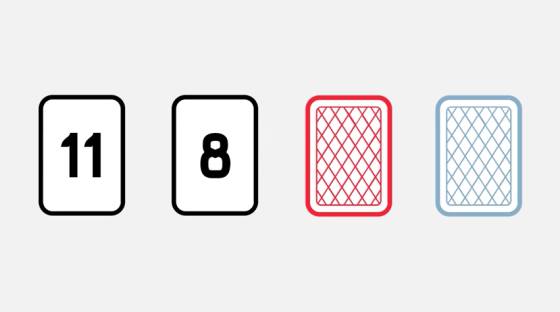
Y ahora, la solución. La mayoría tiende a decir que hay que dar la vuelta al 8 y a la carta roja. Pero no: para refutar la frase, necesitamos encontrar una carta par con el dorso azul, por lo que hay que dar la vuelta al 8 y a la azul. Si el dorso de la carta 8 no fuera rojo, se rompería la norma, al igual que si descubrimos que detrás de la carta azul hay un número par.
Nos da igual el color del dorso de la 11 o el número que haya detrás de la carta roja: si es par, confirmaría la norma sin decirnos nada acerca de si el resto de cartas la cumplen, y si es impar, no la refutaría, ya que ese escenario no está prohibido.
Este experimento de Wason muestra lo mucho que nos dejamos llevar por el sesgo de confirmación: tendemos a buscar las pruebas que confirman una teoría y no tanto las que podrían refutarla, como recuerda Scientific American en este artículo. Por eso se prefiere dar la vuelta al 8, lo cual tiene sentido, pero también se opta más a menudo por la carta roja que por la azul.
¿No lo ves claro? Tomemos una copa (hipotética)
Como explica el vídeo, hay otro aspecto muy interesante de este problema. Si proporcionamos contexto, nos resulta más fácil resolverlo (y entenderlo). Se ve más claro en la segunda versión propuesta. En esta variante hay cartas con edades y bebidas: tenemos que averiguar si hay algún menor de edad tomando alcohol.
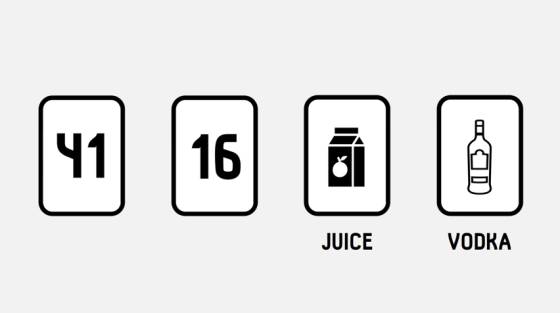
Nos cuesta menos ver que tenemos que dar la vuelta al 16 y al vodka, ya que nos da igual quién beba zumo y qué esté bebiendo la persona de 41 años.
Los autores de esta variante fueron los psicólogos de la Universidad de Florida Richard Griggs y James Cox, en un estudio de 1982 en el que acertaba el 73% de los participantes. Su explicación era que nuestros cerebros están mejor adaptados para el pensamiento concreto que para el abstracto. También ayudaría la familiaridad: la mayoría de nosotros tenemos más experiencia con bares que con los problemas de lógica. No estamos necesariamente orgullosos, pero es así.
No es el único experimento que cambiaba el contexto y mostraba esta mejora en los resultados. De hecho, el propio Wason lo puso a prueba junto con Diana Shapiro ya en 1971, llevando a un escenario concreto estas normas del tipo “si p, entonces q”.
En este caso, se mostraban dos cartas con nombres de ciudades y otras dos con medios de transporte. La prueba consistía en confirmar o desmentir frases como “cada vez que voy a Manchester, lo hago en coche”. 10 de los 16 participantes la resolvieron sin problemas, frente a los 2 de 16 que acertaron en el caso de la versión abstracta.
Más adelante, Leda Cosmides y John Tooby de la Universidad de California propusieron una respuesta basada en la psicología evolutiva a por qué se nos da mejor la segunda versión del problema. Nuestros cerebros tendrían un “sistema de detección de trampas en el cerebro”, como escribe Carl Zimmer en Discover Magazine. El objetivo: identificar a los que incumplen las normas para mantener el orden social, sobre todo en los pequeños grupos en los que vivíamos hace miles de años.
Esta propuesta ha sido muy discutida, recuerda Zimmer, ya que estaría deduciendo demasiadas cosas de un acertijo (por complejo que sea) y el cerebro no se puede dividir en módulos de forma tan clara.
También se han propuesto explicaciones (con sus versiones de este problema) que sugieren que se trata de un error en la interpretación de las normas y el lenguaje. Es decir, muchos dan por supuesto que si la carta tiene un número impar, ha de tener un dorso azul, a pesar de que nadie ha dicho tal cosa en ningún momento.
Tomado de: Verne.